Bolsa
Modelos GARCH: como analisar a volatilidade de ações
Os modelos GARCH (Generalized Autoregressive Conditional Heteroskedasticity) representam uma ferramenta valiosa e indispensável para a gestão de riscos e a avaliação de instrumentos financeiros complexos, como as opções.
Sua aplicação é vital no contexto da análise de séries temporais, especialmente para o estudo da volatilidade dos ativos financeiros.
O que são os modelos GARCH?
Os modelos GARCH são modelos estatísticos, da família dos modelos autorregressivos condicionais heterocedásticos (ARCH, por suas siglas em inglês), utilizados na análise de séries temporais.
Em finanças, os modelos GARCH são utilizados para modelar preços, retornos e volatilidades dos retornos dos ativos financeiros. Portanto, os modelos GARCH permitem modelar e prever a volatilidade flutuante nas séries temporais de instrumentos financeiros, como por exemplo nos rendimentos das ações.
Uma das vantagens do modelo GARCH é que não assume uma variância com valor constante (daí provém o “H”, por heterocedasticidade), estimando a variância com informações passadas (graças a essa qualidade o modelo é autorregressivo e desse conceito toma as iniciais “AR”). Seu principal objetivo é capturar as aglomerações ou clusters de volatilidade, o que significa que períodos de alta volatilidade tendem a ser seguidos por outros de alta volatilidade, e o mesmo ocorre com períodos de baixa volatilidade (daí a ideia de condicionalidade e a letra “C”).
Por último, a diferença entre os modelos ARCH e GARCH reside no fato de que estes últimos não apenas usam os erros passados para prever a variância futura, mas também ampliam (generalizam, daí o “G”) a variância passada em sua previsão, permitindo capturar padrões de volatilidade mais duradouros e de maneira mais eficiente.
Significado de GARCH
A sigla GARCH resume as principais características do modelo:
- Generalized (Generalizado): considera tanto observações recentes como históricas.
- Autoregressive (Autorregressivo): a variável dependente se regrede em si mesma.
- Conditional (Condicional): a variância futura depende da variância passada.
- Heteroskedastic (Heterocedástico): a variância não é constante, varia conforme as observações.
Essa estrutura permite capturar as chamadas aglomerações de volatilidade: períodos de alta volatilidade tendem a ser seguidos por alta, e o mesmo ocorre com períodos de baixa
Por que aplicar modelos GARCH à análise de ações?
O uso dos modelos GARCH é extensivo nos departamentos de risco das administradoras de fundo de investimento, e sua justificativa repousa nas vantagens de seu uso que estão alinhadas com a obtenção de portfólios eficientes e uma adequada gestão do risco:
- Porque é importante gerir a volatilidade dos portfólios de investimento.
- Permite melhorar a gestão de risco, a alocação de capital e a tomada de decisões sobre as transações de ativos financeiros.
- Permitem analisar a volatilidade com maior precisão.
Como aplicar o modelo de GARCH
A construção de um modelo GARCH(p,q) parte da definição da variância condicional dos retornos de um ativo financeiro.
Assume-se que os retornos flutuam em torno de sua média seguindo uma distribuição aproximadamente normal, com média igual a zero e variância que muda ao longo do tempo. Em termos simples:
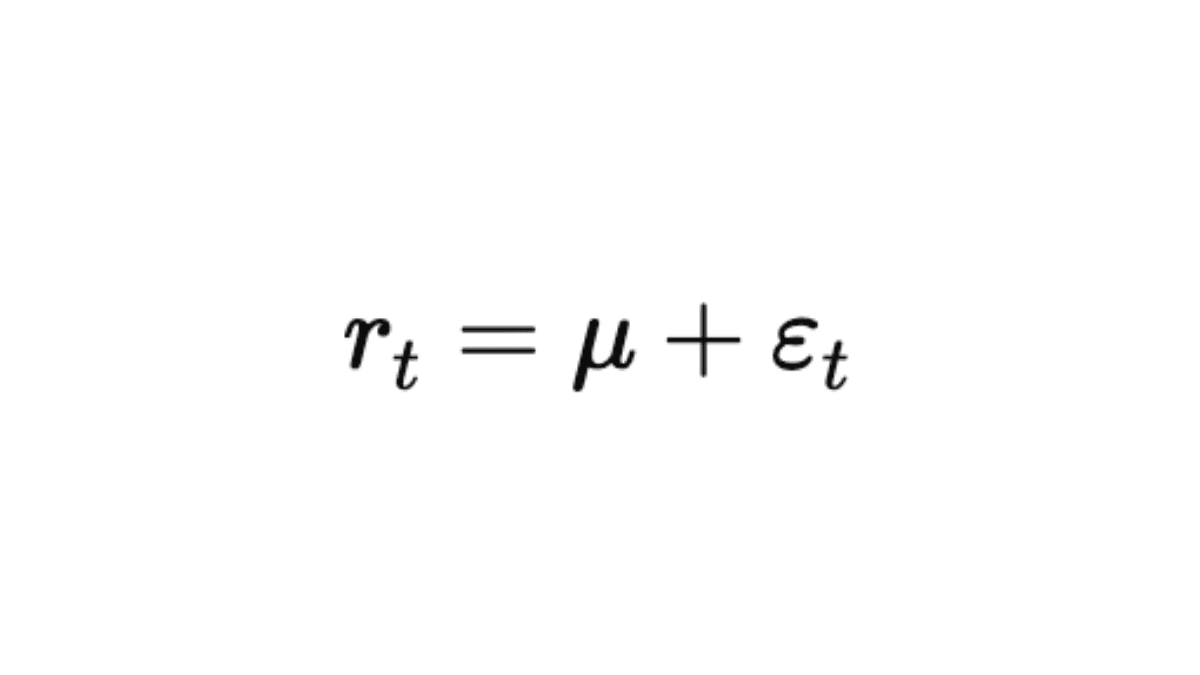
onde εₜ tem média 0 e variância σₜ².
A volatilidade condicional σₜ² não é constante, mas depende de:
- Perturbações ao quadrado (ε²ₜ₋ₚ): choques recentes do mercado.
- Variâncias passadas (σ²ₜ₋q): persistência da volatilidade histórica.
A fórmula geral do modelo é:
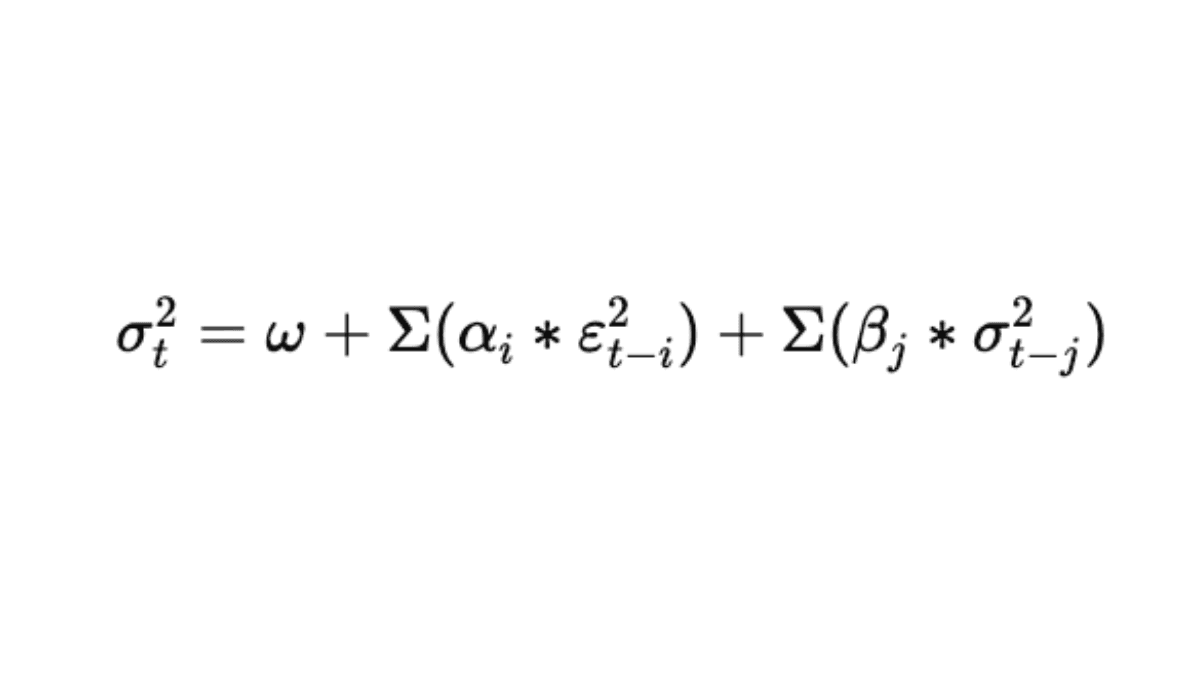
onde:
- ω: termo constante (nível base de volatilidade).
- α: impacto dos choques recentes.
- β: persistência da volatilidade passada.
Variança histórica: na prática, a construção do modelo também parte da variância histórica de um período inicial (como termo constante), incorporando a importância das perturbações passadas no cálculo.
Os parâmetros são estimados via Máxima Verossimilhança, geralmente usando softwares como R, Python, Matlab ou EViews.
Exemplo prático
Suponhamos que queremos prever a volatilidade de uma ação mineradora brasileira para 2025 com dados de 2005 até 2024. Aplicando um GARCH(1,1), obtemos:
- ω=0,03
- α=0,10
- β=0,88
O modelo fica:
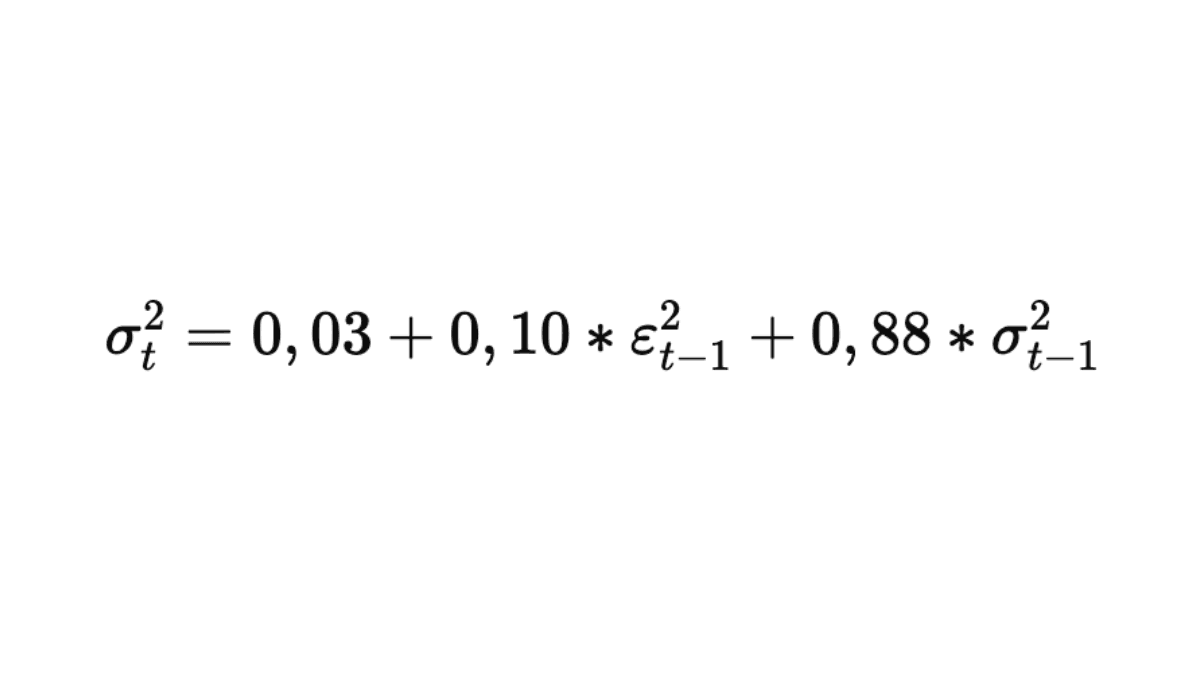
Isso significa que 10% da volatilidade atual vem de choques recentes e 88% da volatilidade passada. A estimativa resultante sugere uma volatilidade anualizada de 15% a 17% para 2025.
Exemplo histórico adicional: em estudos anteriores, como no caso da ação AlpineSki (1984–2019), um GARCH(1,1) estimou volatilidade para 2020 próxima de 16,6%, reforçando a aplicabilidade do método em diferentes mercados.
Tipos de modelos GARCH mais utilizados
Embora o modelo GARCH (1,1) seja a formulação canônica e mais utilizada por sua eficiência e parcimônia, o modelo original apresenta certas limitações, como a suposição de simetria no impacto dos shocks (os impactos positivos e negativos afetam igualmente a volatilidade) e a dificuldade para lidar com certas não-estacionariedades.
Para superar essas deficiências e capturar fenômenos mais complexos e realistas do mercado, como o efeito alavancagem (onde as notícias negativas impactam mais do que as positivas), foram desenvolvidas extensões do modelo GARCH.
A seguir, são apresentadas algumas das variantes mais importantes e sua aplicação na prática financeira:
| GARCH | Versão simétrica padrão. | ||
| A-GARCH | GARCH assimétrico, captura impactos diferentes de choques positivos/negativos. | ||
| GJR-GARCH | GARCH com limiar (threshold), útil para modelar efeito alavancagem. | ||
| E-GARCH | GARCH exponencial, permite modelar efeitos assimétricos e variáveis não estacionárias. | ||
| TGARCH | Considera choques positivos e negativos de forma diferenciada. | ||
| O-GARCH | Ortogonal, usado para ativos correlacionados (ex.: curvas de juros). | ||
| O-EWMA | Ortogonal exponencial com média móvel ponderada, aplicável em volatilidades de múltiplos horizontes. | ||
| GARCH-VAR | Combina vetores autorregressivos com variâncias condicionais. |
| Modelo | Definição |
|---|---|
| GARCH | Versão simétrica padrão. |
| A-GARCH | GARCH assimétrico, captura impactos diferentes de choques positivos/negativos. |
| GJR-GARCH | GARCH com limiar (threshold), útil para modelar efeito alavancagem. |
| E-GARCH | GARCH exponencial, permite modelar efeitos assimétricos e variáveis não estacionárias. |
| TGARCH | Considera choques positivos e negativos de forma diferenciada. |
| O-GARCH | Ortogonal, usado para ativos correlacionados (ex.: curvas de juros). |
| O-EWMA | Ortogonal exponencial com média móvel ponderada, aplicável em volatilidades de múltiplos horizontes. |
| GARCH-VAR | Combina vetores autorregressivos com variâncias condicionais. |
Aplicação modelo GARCH com ações brasileiras
Será aplicado o modelo GARCH a uma ação brasileira que está listada na B3 e cujo foco é a produção e comercialização de produtos da mineração, principalmente nutrientes vegetais, lítio, iodo e potássio.
- Coleta de dados: nesta ocasião foi utilizado o software de programação Rstudio para realizar a leitura e processamento dos dados. Os dados correspondem ao período: 01 de janeiro de 2020 até 23 de setembro de 2025.
- Calculam-se os retornos da série de preços das ações ajustados (ao pagamento de dividendos e divisões) e se plota a série de retornos:
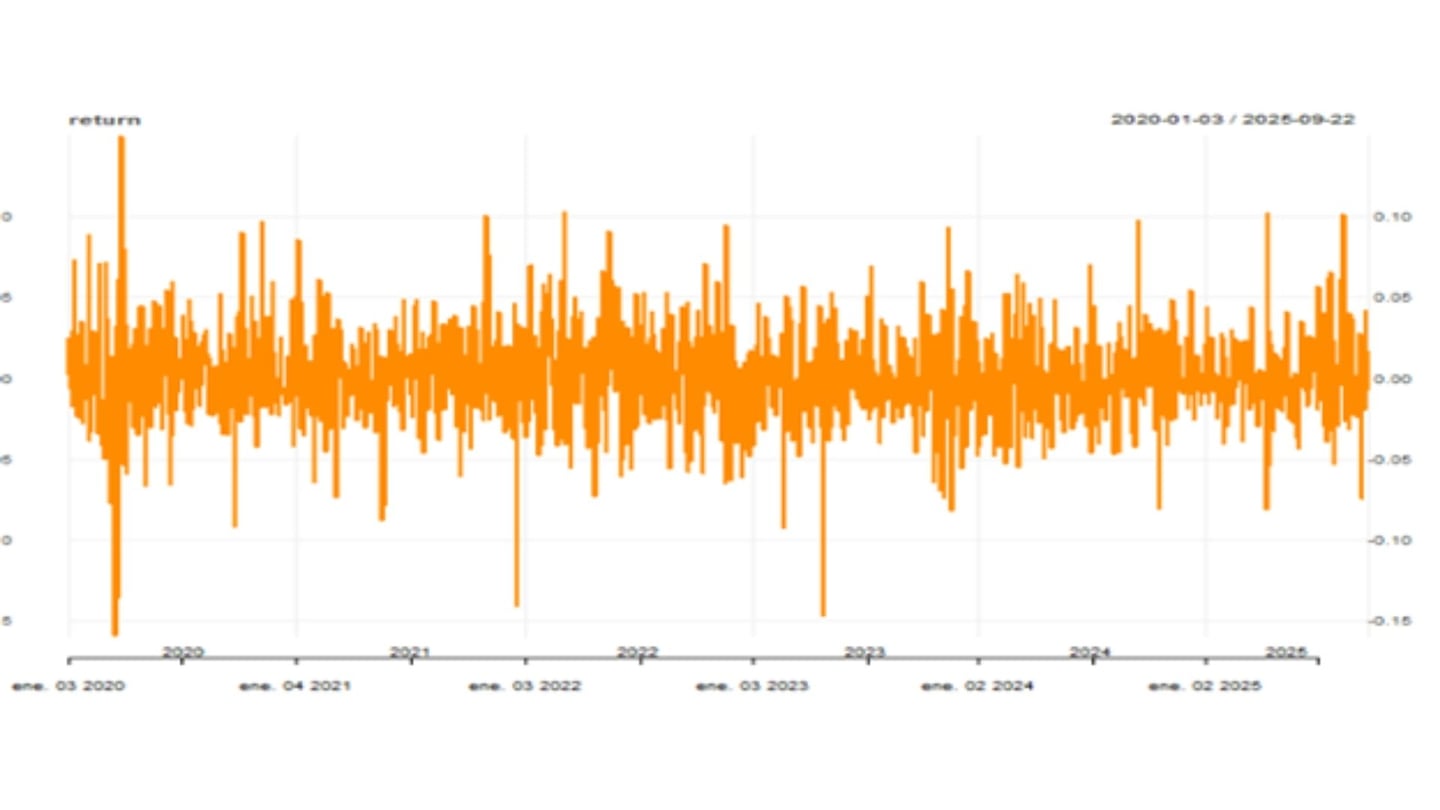
O leitor poderá perceber que o gráfico anterior nos mostra vários períodos onde a volatilidade dos retornos é alta, e que parece acentuar-se o movimento quando o choque é negativo e o rendimento está em queda.
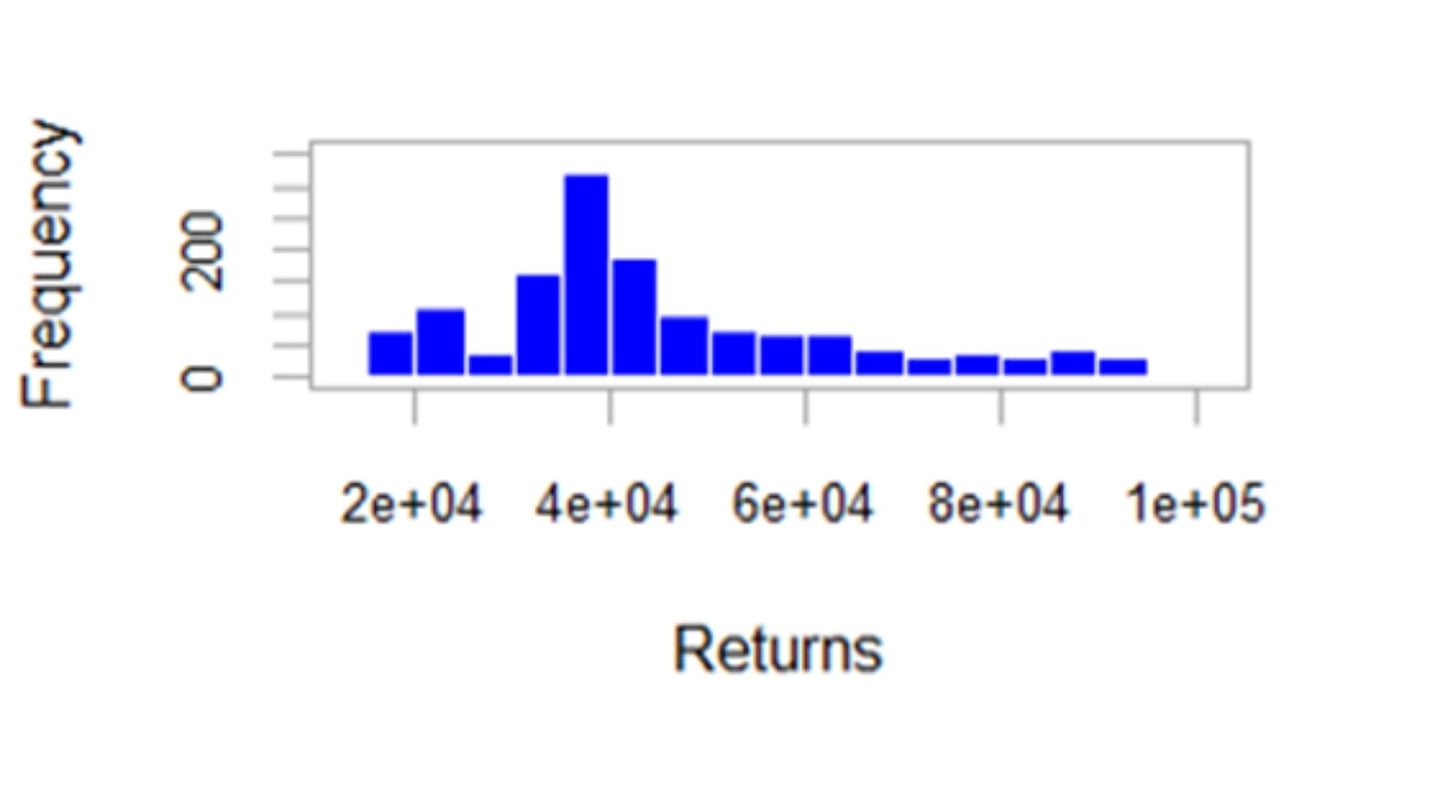
Um dos pressupostos fortes dos modelos GARCH é que se assume normalidade na série de retornos. Assim, o gráfico do histograma nos mostra que a distribuição é assimétrica e que parece ter caudas mais largas do que o esperado.
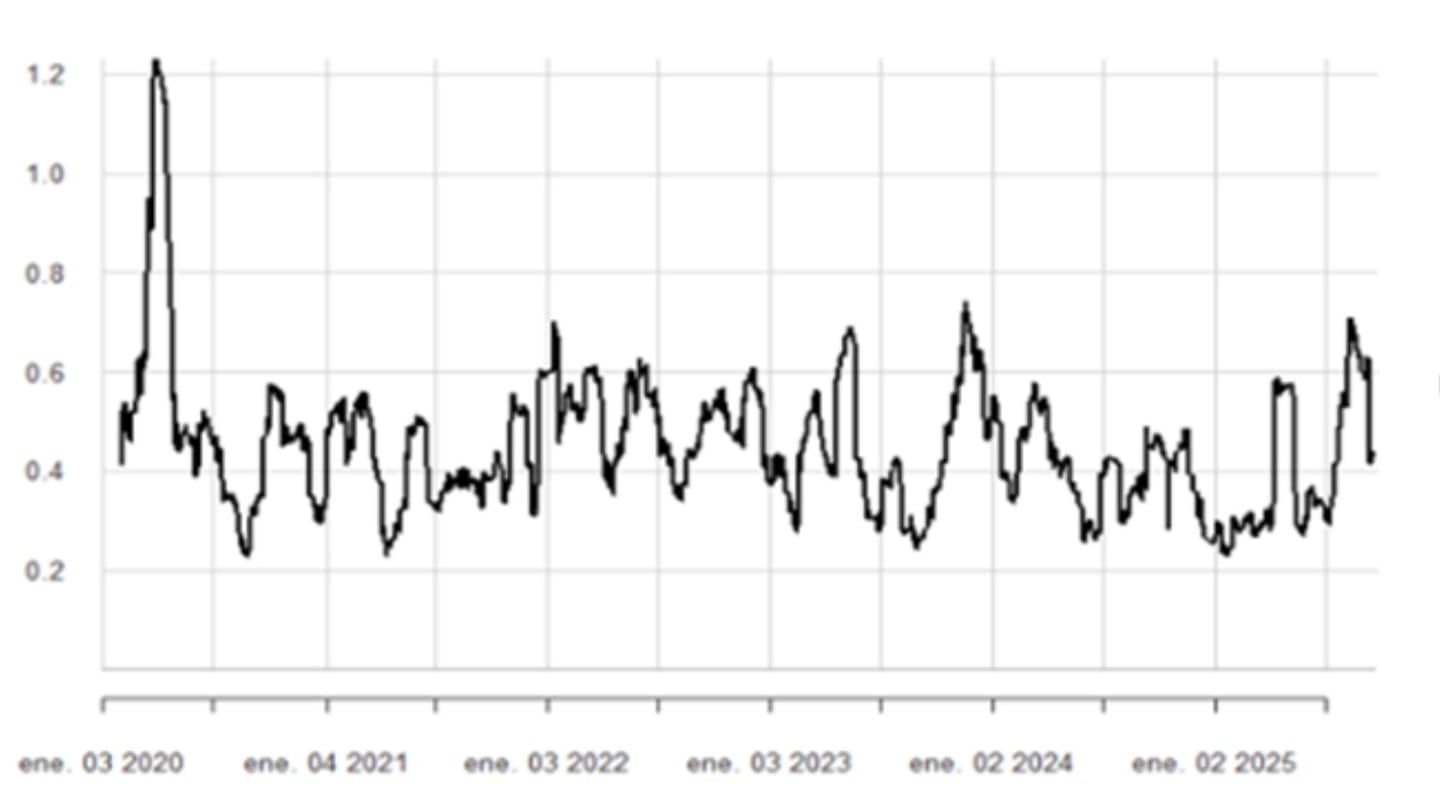
Destaca-se o alto nível de volatilidade do primeiro trimestre de 2020, explicado, principalmente, pelo choque externo da pandemia.
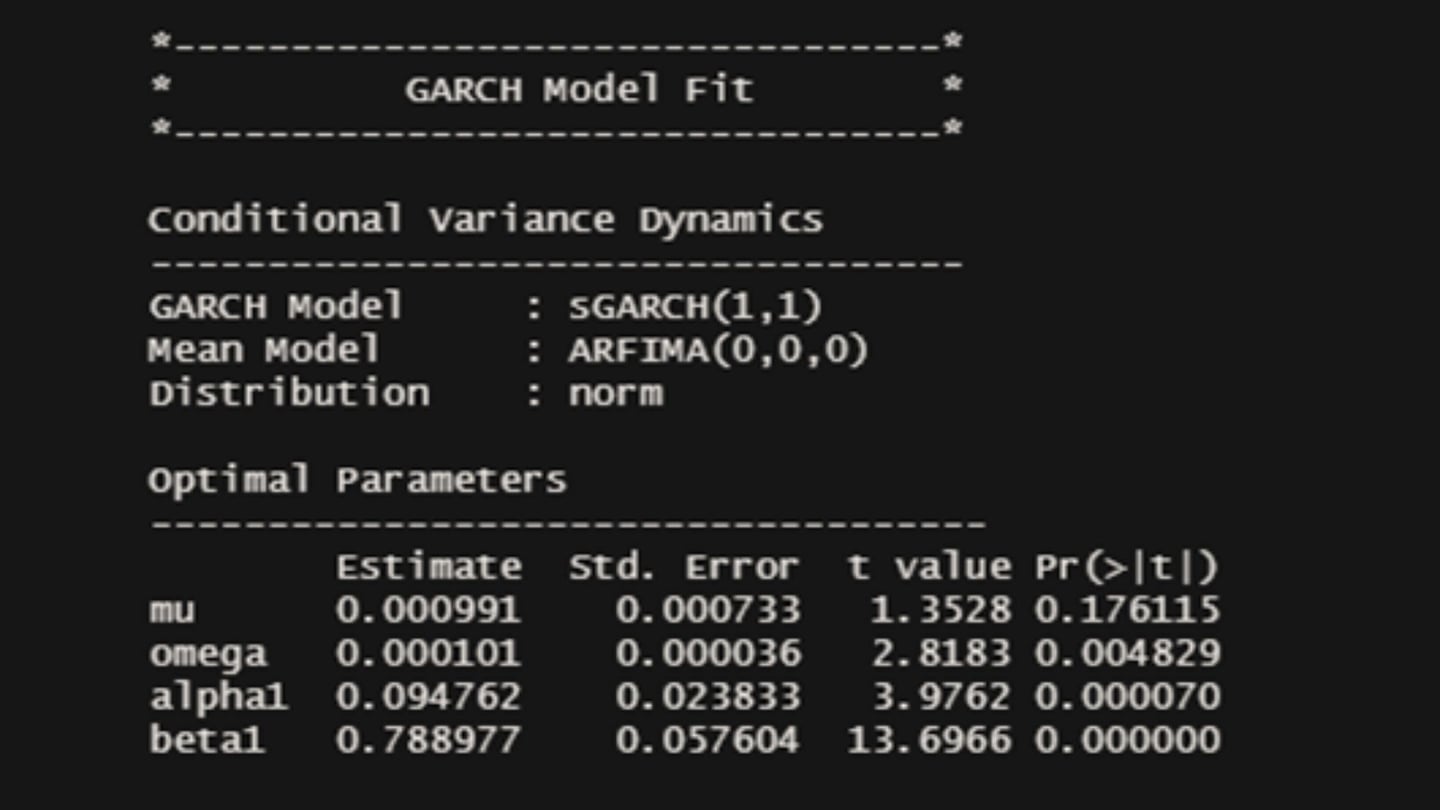
Observa-se que o modelo proposto representa o clássico GARCH(1,1), ou seja, que na previsão da variância influencia o atraso dos erros e da própria variância, em um único período anterior.
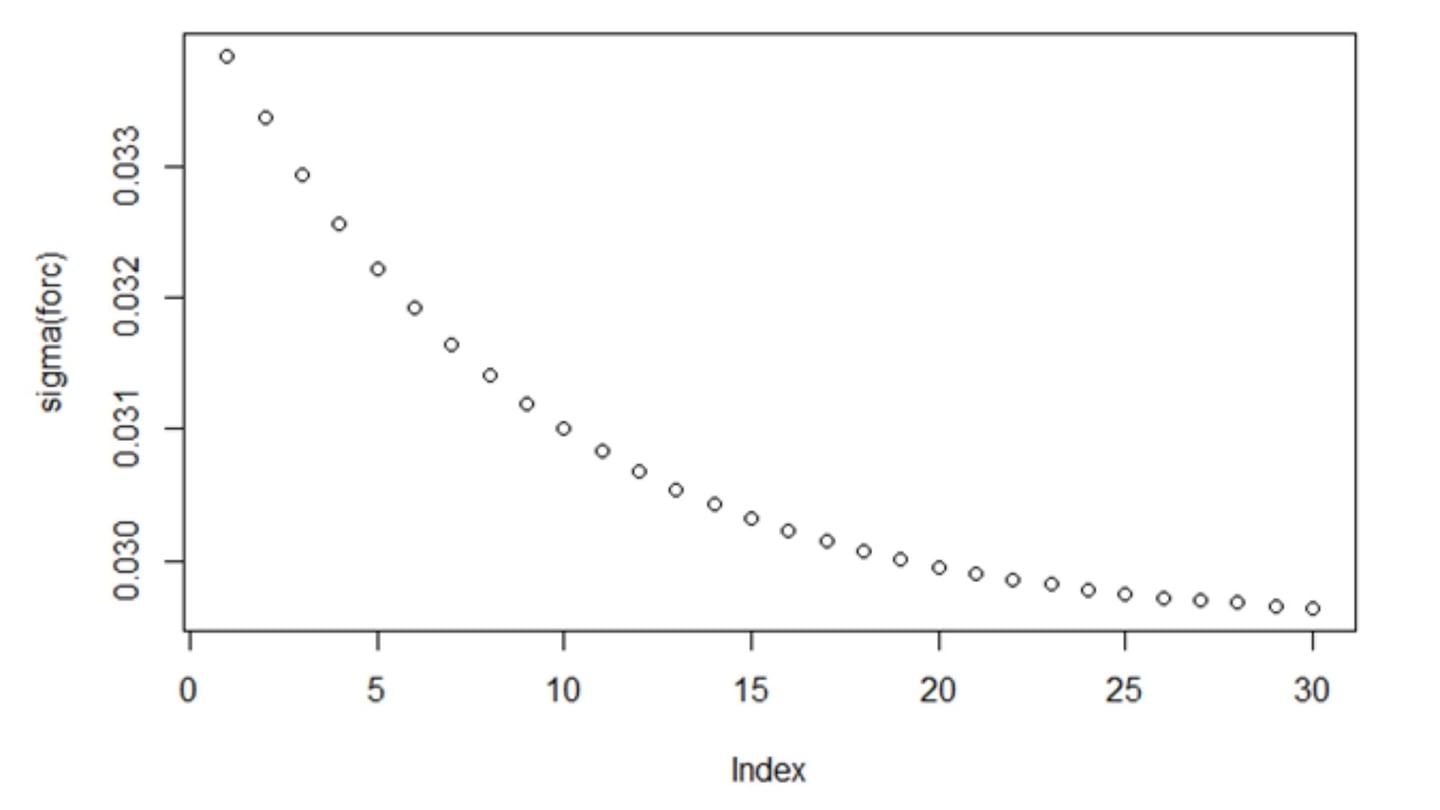
Com tudo, a previsão da volatilidade para os próximos 30 dias, em função desta aplicação do modelo GARCH, é que diminua continuamente. Cabe destacar que este exercício é meramente um exemplo teórico e não constitui em nenhum caso um conselho ou recomendação de transação (compra ou venda) sobre a ação exposta neste exemplo.
Como usar GARCH em decisões de investimento
Como qualquer aplicação de uma teoria, o uso de modelos GARCH requer a execução ordenada de passos sequenciais, que a seguir serão descritos:
| Elaboração de base de dados | Construção da base de dados do portfólio de investimentos. Coletam-se os dados dos preços dos ativos financeiros e calculam-se os retornos logarítmicos dos preços dos ativos. | ||
| Estimativa do modelo GARCH | Uso de um modelo GARCH (ou qualquer de sua família, ver tabela anterior) para prever a volatilidade. | ||
| Previsões da volatilidade | Uso dos modelos GARCH para prever a volatilidade futura dos ativos financeiros. | ||
| Aplicações | 1. Criação de portfólios, incorporando a volatilidade para a construção de portfólios eficientes. 2. Gestão de riscos, estimativa do risco e aplicação de estratégias de mitigação. 3. Valoração de opções, input para modelos de valoração de opções financeiras. |
| Etapas na Modelagem GARCH: | Descrição: |
|---|---|
| Elaboração de base de dados | Construção da base de dados do portfólio de investimentos. Coletam-se os dados dos preços dos ativos financeiros e calculam-se os retornos logarítmicos dos preços dos ativos. |
| Estimativa do modelo GARCH | Uso de um modelo GARCH (ou qualquer de sua família, ver tabela anterior) para prever a volatilidade. |
| Previsões da volatilidade | Uso dos modelos GARCH para prever a volatilidade futura dos ativos financeiros. |
| Aplicações | 1. Criação de portfólios, incorporando a volatilidade para a construção de portfólios eficientes. 2. Gestão de riscos, estimativa do risco e aplicação de estratégias de mitigação. 3. Valoração de opções, input para modelos de valoração de opções financeiras. |
